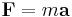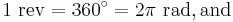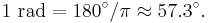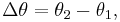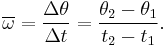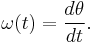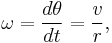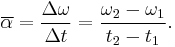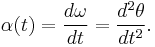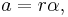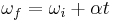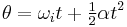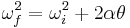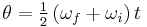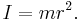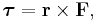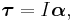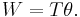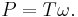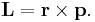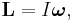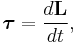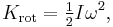Rotation around a fixed axis
Rotation around a fixed axis is a special case of rotational motion. The fixed axis hypothesis exclude the possibility of a moving axis, and cannot describe such phenomena as wobbling or precession. According to Euler's rotation theorem, simultaneous rotation around more than one axis at the same time is impossible. If two rotations are forced at the same time, a new axis of rotation will appear.
The kinematics and dynamics of rotation around a fixed axis of a rigid body are mathematically much simpler than those for free rotation of a rigid body; they are entirely analogous to those of linear motion along a single fixed direction, which is not true for free rotation of a rigid body. The expressions for the kinetic energy of the object, and for the forces on the parts of the object, are also simpler for rotation around a fixed axis, than for general rotational motion. For these reasons, rotation around a fixed axis is typically taught in introductory physics courses after students have mastered linear motion; the full generality of rotational motion is not usually taught in introductory physics classes.
Contents |
Translation and rotation
Kinematics
Angular Displacement
A particle moves in a circle of radius  . Having moved an arc length
. Having moved an arc length  , its angular position is
, its angular position is  relative to its original position, where
relative to its original position, where 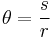 .
.
In mathematics and physics it is usual to use the natural unit radians rather than degrees or revolutions. Units are converted as follows:
An angular displacement is a change in angular position:
where 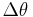 is the angular displacement,
is the angular displacement, 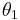 is the initial angular position and
is the initial angular position and 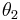 is the final angular position.
is the final angular position.
Angular speed and angular velocity
Angular velocity is the change in angular displacement per unit time. The symbol for angular velocity is  and the units are typically rad s-1. Angular speed is the magnitude of angular velocity.
and the units are typically rad s-1. Angular speed is the magnitude of angular velocity.
The instantaneous angular velocity is given by
Using the formula for angular position and letting 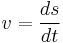 , we have also
, we have also
where  is the translational speed of the particle.
is the translational speed of the particle.
Angular velocity and frequency are related by
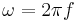 .
.
Angular acceleration
A changing angular velocity indicates the presence of an angular acceleration in rigid body, typically measured in rad s−2. The average angular acceleration 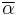 over a time interval Δt is given by
over a time interval Δt is given by
The instantaneous acceleration α(t) is given by
Thus, the angular acceleration is the rate of change of the angular velocity, just as acceleration is the rate of change of velocity.
The translational acceleration of a point on the object rotating is given by
where r is the radius or distance from the axis of rotation. This is also the tangential component of acceleration: it is tangential to the direction of motion of the point. If this component is 0, the motion is uniform circular motion, and the velocity changes in direction only.
The radial acceleration (perpendicular to direction of motion) is given by
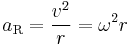 .
.
It is directed towards the center of the rotational motion, and is often called the centripetal acceleration.
The angular acceleration is caused by the torque, which can have a positive or negative value in accordance with the convention of positive and negative angular frequency. The ratio of torque and angular acceleration (how difficult it is to start, stop, or otherwise change rotation) is given by the moment of inertia: 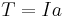 .
.
Equations of kinematics
When the angular acceleration is constant, the five quantities angular displacement  , initial angular velocity
, initial angular velocity 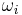 , final angular velocity
, final angular velocity 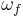 , angular acceleration
, angular acceleration  , and time
, and time  can be related by four equations of kinematics:
can be related by four equations of kinematics:
Dynamics
Moment of inertia
The moment of inertia of an object, symbolized by I or J, is a measure of the object's resistance to changes to its rotation. The moment of inertia is measured in kilogram metre² (kg m²). It depends on the object's mass: increasing the mass of an object increases the moment of inertia. It also depends on the distribution of the mass: distributing the mass further from the centre of rotation increases the moment of inertia by a greater degree. For a single particle of mass  a distance
a distance  from the axis of rotation, the moment of inertia is given by
from the axis of rotation, the moment of inertia is given by
Torque
Torque τ is the twisting effect of a force F applied to a rotating object which is at position r from its axis of rotation. Mathematically,
where × denotes the cross product. A net torque acting upon an object will produce an angular acceleration of the object according to
just as F = ma in linear dynamics.
The work done by a torque acting on an object equals the magnitude of the torque times the angle through which the torque is applied:
The power of a torque is equal to the work done by the torque per unit time, hence:
Angular Momentum
The angular momentum L is a measure of the difficulty of bringing a rotating object to rest. It is given by
Angular momentum is related to angular velocity by
just as p = mv in linear dynamics.
Torque and angular momentum are related according to
just as F = dp/dt in linear dynamics. In the absence of an external torque, the angular momentum of a body remains constant. The conservation of angular momentum is notably demonstrated in figure skating: when pulling the arms closer to the body during a spin, the moment of inertia is decreased, and so the angular velocity is increased.
Kinetic energy
The kinetic energy Krot due to the rotation of the body is given by
just as Ktrans = 1⁄2mv2 in linear dynamics.
Vector expression
The above development is a special case of general rotational motion. In the general case, angular displacement, angular velocity, angular acceleration and torque are considered to be vectors.
An angular displacement is considered to be a vector, pointing along the axis, of magnitude equal to that of 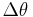 . A right-hand rule is used to find which way it points along the axis; if the fingers of the right hand are curled to point in the way that the object has rotated, then the thumb of the right hand points in the direction of the vector.
. A right-hand rule is used to find which way it points along the axis; if the fingers of the right hand are curled to point in the way that the object has rotated, then the thumb of the right hand points in the direction of the vector.
The angular velocity vector also points along the axis of rotation in the same way as the angular displacements it causes. If a disk spins counterclockwise as seen from above, its angular velocity vector points upwards. Similarly, the angular acceleration vector points along the axis of rotation in the same direction that the angular velocity would point if the angular acceleration were maintained for a long time.
The torque vector points along the axis around which the torque tends to cause rotation. To maintain rotation around a fixed axis, the total torque vector has to be along the axis, so that it only changes the magnitude and not the direction of the angular velocity vector. In the case of a hinge, only the component of the torque vector along the axis has effect on the rotation, other forces and torques are compensated by the structure.
Examples and applications
Constant angular speed
The simplest case of rotation around a fixed axis is that of constant angular speed. Then the total torque is zero. For the example of the Earth rotating around its axis, there is very little friction. For a fan, the motor applies a torque to compensate for friction. The angle of rotation is a linear function of time, which modulo 360° is a periodic function.
An example of this is the two-body problem with circular orbits.
Centripetal force
Internal tensile stress provides the centripetal force that keeps a spinning object together. A rigid body model neglects the accompanying strain. If the body is not rigid this strain will cause it to change shape. This is expressed as the object changing shape due to the "centrifugal force".
Celestial bodies rotating about each other often have elliptic orbits. The special case of circular orbits is an example of a rotation around a fixed axis: this axis is the line through the center of mass perpendicular to the plane of motion. The centripetal force is provided by gravity, see also two-body problem. This usually also applies for a spinning celestial body, so it need not be solid to keep together, unless the angular speed is too high in relation to its density. (It will, however, tend to become oblate.) For example, a spinning celestial body of water must take at least 3 hours and 18 minutes to rotate, regardless of size, or the water will separate. If the density of the fluid is higher the time can be less. See orbital period.
See also
References
Further reading
Concepts of Physics Volume 1, 1st edition Seventh reprint by Harish Chandra Verma ISBN 81-7709-187-5